Skull Cavern/Ore Distribution

Small minable stones and ores can appear as random stones throughout the floor, or rarely as small clumps. These have different distributions. On average there will be less than 0.67 small resource clumps on each floor with neutral luck, and less than 1 for the largest possible luck. These clumps have a 25% chance to be a dark grey rock (stone ore), a 1.5% chance to be iridium, and a 73.5% chance to be gold.

The distribution for random stones is more complex and varies with depth and best understood in a few stages.

If a Qi quest is in progress which makes the mine more dangerous, there is a small chance for a stone to be replaced with a radioactive node. This is very dependent upon luck, with the luck boost from the special charm being worth 192 floors, and the worst luck requiring a depth of floor 550 to have any chance ore will drop. This is also dependent on luck buffs, with each level of luck worth 15 floors. This will replace any of the below stones.

The chance for a stone to be a metal ore (copper, iron, gold, or iridium) will vary depending on floor, starting at 2% on floor 1, rapidly increasing to 16% on floor 100, and then increasing to 100% on floor 1780. Luck has no effect on this chance, or on the ore distribution. Copper and iron have the same distribution. From floor 2010 only gold and iridium ore will be found, and from floor 5700 only iridium ore will be found from this generation.

If the stone is not a metal ore, there is a chance for it to be a a gem stone ore (diamond, emerald, aquamarine, ruby, amethyst, topaz, and jade), a gem node (the round purple stone), a mystic stone or a dark grey rock. This means that the chance can decrease as you go deeper as more of the stone is metal ore, and above floor 1780 these will not be found. Luck and mining level only play a significant role for mystic stones and gem nodes. For others the contribution is negligible.

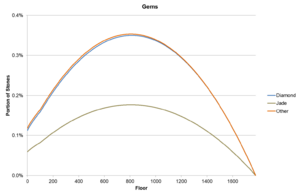
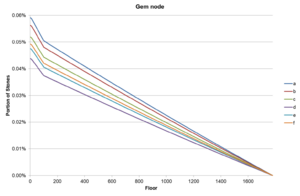
For gem stone ores, diamond is slightly rarer than most, and jade is twice as rare as most. The chance initially increases, peaking at a chance of ~0.35% (~0.18% for jade) at a depth of ~800, before dropping back down.

Dark grey rocks, start with their maximum chance at floor 1 (9.73% for dark grey rocks, 0.005% for mystic stones, 0.059% for gem nodes for best chances), and drop proportionally as ores take their place.

During the Desert Festival, there are some small changes to how the ore is generated, this is to allow the generation of Calico egg nodes. This occurs below in the section to generate ore clumps, and the section to generate metallic ores.

Code Details

The main code for populating the floor is found in the function StardewValley.Locations.MineShaft::populateLevel. In setting up to populate the floor, it initially defines stoneChance as a random number (double) in the range [10,30), and gemStoneChance as 0.003. It then calls StardewValley.Locations.MineShaft::adjustLevelChances, which will perform a few checks including setting the chance to find stone to 0 for infested floors and dividing gem stone chance by 2. After this setup, it will then iterate through every square of the floor, and if it passes a few checks it will add a stone selected using the function StardewValley.Locations.MineShaft::createLitterObject, passing the gemstone chance from above and the magic numbers 0.001 and 5e-5 for gem nodes (internally chanceForPurpleStone) and mystic stones (internally chanceForMysticStone). In the same sweep, if it does not add a stone there is a chance for it to add a large resource clump, which are 2 possible variants of a 2 by 2 boulder.

After iterating through every square, and performing a few other tasks, it will attempt to add ore clumps using the function StardewValley.Locations.MineShaft::tryToAddOreClumps, but only if the floor is not divisible by 5, and it is not a treasure room.

Ore Clumps

In the StardewValley.Locations.MineShaft::tryToAddOreClumps function, a try will only be made if a random number is less than 0.55 plus the average daily luck. The maximum possible average daily luck is 0.1 from random luck and 0.025 from the special charm. This means with neutral luck there is a 55% chance to try, and with the best possible luck there is a 67.5% chance. It will try once, and then generate a random number and keep going if that random number is less than 0.25 plus the average daily luck. This means there will be 1 chance, plus a 25% chance with neutral luck or a 37.5% chance with best possible luck.

This gives an expected value of 1.3 recurring or 1.6 attempts to generate a clump, which when combined with the base chance to try gives an expected amount of 0.67 or 1.

However, each try chooses a random tile on the map and will only place an ore clump there if the tile is free, resulting in less than these numbers.

To choose which type of ore to add it calls the function StardewValley.Locations.MineShaft::getAppropriateOre, which just before returning has a 25% chance (if it is not in hard mode) to set the ore to 668 or 670, which are the dark grey rocks (stone ore).

Otherwise, it first checks if the Desert Festival is ongoing. If it is there is a (25 + "Egg Rating" / 20)% chance of the node being a Calico egg node. Otherwise, the ore is set as 764, gold ore, with a 2% chance to set it to 765, iridium ore.

When the festival is not ongoing, this results in total chances of 25% for dark grey rocks, 1.5% chance for iridium ore, and 73.5% for gold.

Random ore placement (createLitterObject)

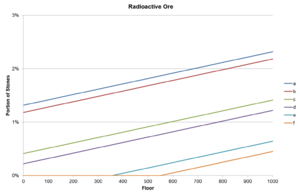
Radioactive Ore

Changing distribution of radioactive ore with luck (daily luck and luff buffs) with a difficulty of 1.

This will first produce radioactive ore, with the following check:

if (this.GetAdditionalDifficulty() > 0 && this.mineLevel % 5 != 0 && this.mineRandom.NextDouble() < (double)this.GetAdditionalDifficulty() * 0.001 + (double)((float)this.mineLevel / 100000f) + Game1.player.team.AverageDailyLuck() / 13.0 + Game1.player.team.AverageLuckLevel() * 0.0001500000071246177)

The difficulty can be changed by using the statue at the cavern entrance or by accepting the Qi quest Skull Cavern Invasion. This provides 3 levels, normal (0), one of these active (1), or both of these active (2). With a difficulty of 0, no radioactive ore will spawn.

The luck boost from the special charm (0.025, contribution to AverageDailyLuck) is equivalent to an additional 192.3 floors (2500/13), and a single point of luck (such as from a food buff) is worth ~15 floors. The boost from the additional difficulty (setting it to 2 instead of 1) is equivalent to 100 floors.

With the difficulty set to 1, with the best possible luck (0.125 daily luck with special charm, +9 luck from magic rock candy, a ginger ale made with Qi seasoning, and 2 lucky rings) 1.32% of stones will be radioactive ore on floor 1, increasing to 1.42% on floor 99. With the worst possible luck no radioactive ore will appear until floor 550. Also note that radioactive ore will not appear on any floor divisible by 5.

This means that hypothetically with the best possible luck, with difficulty set to 2, from floor 98584 onwards, except on floors divisible by 5, the only ore found from random stones would be radioactive ore. With the worst possible luck, this increases to floor 100450. Reaching these floors would require bypassing the Quarry Mine floor, which can be found on floor 77257 of Skull Cavern.

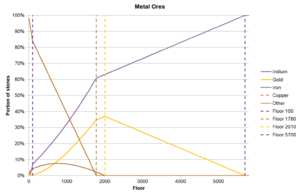
Metal Ores

After this, it will go through the different areas, and for skull cavern, it will set the base stone type to 32, 38, 40 or 42 (equally), and then calculate several variables, in a few stages to give different definitions for different floor ranges chanceForOre is defined in 2 parts, including using a min, and then compared to a random double to give 4 different regions:

    double chanceForOre = 0.02 + (double)skullCavernMineLevel * 0.0005;
    if (this.mineLevel >= 130) {
        chanceForOre += 0.01 * (double)((float)(Math.Min(100, skullCavernMineLevel) - 10) / 10f);
    }

This ends up being defined as either 0.02 + skullCavernMineLevel * 0.0005 for floors 1-10, 0.01 + skullCavernMineLevel * 0.0015 for floors 10 to 100 (when skullCavernMineLevel <= 100), and 0.11 + skullCavernMineLevel * 0.0005 for floors 100 and up(when skullCavernMineLevel >= 100). This means the chance for ore will increase by 0.05% for each floor, except between floors 10 and 100 where it increases by 0.15% each floor. This reaches 100% at floor 1780, providing the 4th region. At the crossover point of floor 10 the 2 chances are equal as the extra term is 0. This means the function is continuous. If this ore check passes it will return an ore.

Changing distribution of metal ore with floor.

First, if the Desert Festival is ongoing. If it is there is a (13 + "Egg Rating" / 20)% chance of the node being an Calico egg node. This will not be included in the below graphs and discussions. After that, it first checking for iridium, then gold, then iron, then returning copper. As an example, this means for a stone to be gold ore it must pass the ore check, then fail the iridium check, then pass the gold check. This means in order to get an ore, the chance for the previous ore must be less than 100%, so once iridium ore reaches 100%, no other metal ores can be made. The probability to get each ore (from a random stone) is therefore:

   iridium = chanceForOre*chanceForIridium
      gold = chanceForOre*(1-chanceForIridium)*chanceForGold
      iron = chanceForOre*(1-chanceForIridium)*(1-chanceForGold)*chanceForIron
    copper = chanceForOre*(1-chanceForIridium)*(1-chanceForGold)*(1-chanceForIron)

These probabilities are defined in the following code:

    double iridiumBoost = 0.0;
    if (this.mineLevel >= 130) {
        iridiumBoost += 0.001 * (double)((float)(skullCavernMineLevel - 10) / 10f);
    }
    iridiumBoost = Math.Min(iridiumBoost, 0.004);
    if (skullCavernMineLevel > 100) {
         iridiumBoost += (double)skullCavernMineLevel / 1000000.0;
    }
    double chanceForIridium = (double)Math.Min(100, skullCavernMineLevel) * (0.0003 + iridiumBoost);
    double chanceForGold = 0.01 + (double)(this.mineLevel - Math.Min(150, skullCavernMineLevel)) * 0.0005;
    double chanceForIron = Math.Min(0.5, 0.1 + (double)(this.mineLevel - Math.Min(200, skullCavernMineLevel)) * 0.005);

The chance to find iridium relies upon an iridiumBoost variable which is split into four regions, floors 0-10, where there is no boost; floors 10 to 50, where the boost increases from 0 to 0.004; floors 50 to 99 where the boost remains constant at 0.004; and floor 100 and up, where there is a discontinuity with the boost jumping to 0.004 + 0.000001 * skullCavernMineLevel (an increase of 0.0001). This results in the overall function for the chance to find iridium being non-linear, and having 5 regions; importantly reaching 100% at floor 5700. The gold ore chance variable is more straight forward, starting at a value of 7%, and once floor 150 is reached, increasing linearly until it reaches 100% at floor 2130. The iron ore chance results in a value of 50%. Additional floors of note are floor 30 where iridium ore becomes more common than gold ore, floor 74 where iridium ore becomes more common than iron and copper ore, floor 677 where gold ore becomes more common than iron and copper ore, floor 1081 where iridium ore becomes more common than non-metal ores, floor 1332 where gold ore becomes more common than non-metal ores, and floor 1725 where iron and copper ore becomes more common than non-metal ores.

Other ores

Additionally, up until this point, luck has not factored into the calculation. However, if it does not pass the ore chance check (this means the final chances for these will need 1-chanceForOre included), it moves on to gemstone ores, dark grey rocks (stone ore), purple stones and mystic stones. This is done in the following complex code (some unneeded sections related to coloured rocks have been removed, and additional comments added):

    double averageDailyLuck = Game1.player.team.AverageDailyLuck(Game1.currentLocation);
    double averageMiningLevel = Game1.player.team.AverageSkillLevel(3, Game1.currentLocation);
    double chanceModifier = averageDailyLuck + averageMiningLevel * 0.005;
    // Diamond node.
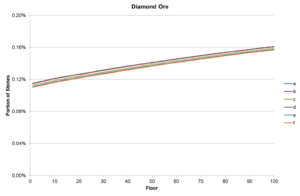
    if (this.mineLevel > 50 && this.mineRandom.NextDouble() < 0.00025 + (double)this.mineLevel / 120000.0 + 0.0005 * chanceModifier / 2.0) {
        whichStone = 2;
        stoneHealth = 10;
    }
    // Gem stone nodes.
    else if (gemStoneChance != 0.0 && this.mineRandom.NextDouble() < gemStoneChance + gemStoneChance * chanceModifier + (double)this.mineLevel / 24000.0) {
        return new Object(tile, this.getRandomGemRichStoneForThisLevel(this.mineLevel), "Stone", canBeSetDown: true, canBeGrabbed: false, isHoedirt: false, isSpawnedObject: false) {
            MinutesUntilReady = 5
        };
    }
    // gem node (purple rocks).
    if (this.mineRandom.NextDouble() < chanceForPurpleStone / 2.0 + chanceForPurpleStone * averageMiningLevel * 0.008 + chanceForPurpleStone * (averageDailyLuck / 2.0)) {
        whichStone = 44;
    }
    // Mystic stones.
    if (this.mineLevel > 100 && this.mineRandom.NextDouble() < chanceForMysticStone + chanceForMysticStone * averageMiningLevel * 0.008 + chanceForMysticStone * (averageDailyLuck / 2.0)) {
        whichStone = 46;
    }
    whichStone += whichStone % 2;
    // Dark grey rock (stone ore).
    if (this.mineRandom.NextDouble() < 0.1 && this.getMineArea() != 40) {
        return new Object(tile, (this.mineRandom.NextDouble() < 0.5) ? 668 : 670, "Stone", canBeSetDown: true, canBeGrabbed: false, isHoedirt: false, isSpawnedObject: false)
        {
            MinutesUntilReady = 2,
            Flipped = (this.mineRandom.NextDouble() < 0.5)
        };
    }
    return new Object(tile, whichStone, "Stone", canBeSetDown: true, canBeGrabbed: false, isHoedirt: false, isSpawnedObject: false)	{
        MinutesUntilReady = stoneHealth
    };

Changing distribution of diamond nodes with floor, luck, and mining level

Before analysing in full, it is worth noting the impact of luck. Diamonds and Gemstones both use chanceModifier. As daily luck ranges from a minimum of -0.1 to a maximum of 0.125 (with special charm), and farmer level ranges from 0 to 14, the lowest this can be is -0.1, and the highest is 0.195. For diamonds this is multiplied by 0.0005 and divided by 2 making its effect range from -0.0025% to 0.004875%, or by approximately 0.007%, equivalent to 8.85 floors. For a farmer with the special charm and level 10 mining, the range is reduced to 0.005%, equivalent to 6.6 floors. This is also quite small compared to the base of 0.126% for floor 1 with 0 luck and 0 mining levels. For gemstone ores, the range works out to be 0.044% for the entire range, or 0.033% for the reduced range; equivalent to 10.62 and 7.92 floors, and still small compared to the 0.654% at floor 1. The chance for gem nodes and mystic stones don't directly use the floor, and the multiplier for the chance is used in all parts of the calculation. Now the range for averageDailyLuck/2 (0.1125) is quite large, over 20% of the base 0.5 chance, making this much more dependent upon luck. Likewise, the 14 levels from mining contribute 0.112, over 10%, but the 4 gained from food buffs only contribute 0.032, much less significant. Likewise, for Mystic Stones the contribution from luck is over 10% of the base of 1, with the mining levels having a similarly reduced impact.

This can be better understood by considering the exit points. The first way to return from this function is by failing the diamond check and passing the gem stone check. The second way is if it fails the above, but passes the dark grey rock check. Otherwise it exits as whatever stone it was last set to (so mystic first, then purple, then diamond, then regular stone). This can be understood as (where each check is if they pass the check for meeting the chance):

   if (!diamondCheck && gemCheck){
       return gem
   }
   if (stoneCheck) {
       return grey rock
   }
   if (mysticCheck) {
       return mystic stone
   }
   if (purpleCheck) {
       return gem node
   }
   if (diamondCheck) {
       return diamond
   }
   return rock

However the use of diamondCheck twice means you cannot just use the chance for it twice, as it will either pass both times or fail both times, making calculations of chances more complex. The simplest to understand is the gemstone ore. In order to return the gemstone ore, the diamond check must fail, and the gem check must pass. This is equivalent to:

   (1-chanceForOre)*(1-chanceForDiamond)*chanceForGem.

Additionally, this returns a random gem using the function MineShaft::getRandomGemRichStoneForThisLevel. This relies upon the code:

    int whichGem = this.mineRandom.Next(59, 70);
    whichGem += whichGem % 2;

Changing distribution of gemstone nodes with floor with neutral base luck, the special charm and level 10 mining.

Which will randomly select an integer in the range [59,70), and then add 1 if it is odd. This has the effect of randomly selecting an even integer from 60 to 70 inclusive, with the integers from 60 to 68 inclusive having an equal likelihood and 70 being half as likely. This is because the mineRandom.Next(a,b) will return an integer greater than or equal to a and less than b, from internally generating a random number from 0 to 1, scaling it and offsetting it to be a random decimal number from 59 to 70, and then rounding down. This means that the range 59 to just below 61 will round to 59 or 60, which is then both forced to 60; while the numbers from 69 to 70 will round to 69 and then be converted to 70, meaning 70 has half the range. This means that the chance for jade (from 70) will be one 11th of the chance to obtain a gem, and the other gems (emerald, aquamarine, ruby, amethyst, and topaz) will be double that:

      jade = (1-chanceForOre)*(1-chanceForDiamond)*chanceForGem/11
     other = (1-chanceForOre)*(1-chanceForDiamond)*chanceForGem*2/11

Changing distribution of gem nodes with floor luck and mining level.

The chance to not be a gem stone ore, and be some other option (other than diamond) relies upon either passing the diamond check, or failing the diamond check and failing the gemstone check. This chance is equal to:

   chanceForDiamond+(1-chanceForDiamond)*(1-chanceForGem) = 1-(1-chanceForDiamond)*chanceForGem

Then going through each return statement we have the final chances being:

     stone = (1-chanceForOre)*(1-(1-chanceForDiamond)*chanceForGem)*chanceForStone
    mystic = (1-chanceForOre)*(1-(1-chanceForDiamond)*chanceForGem)*(1-chanceForStone)*chanceForMystic
    purple = (1-chanceForOre)*(1-(1-chanceForDiamond)*chanceForGem)*(1-chanceForStone)*(1-chanceForMystic)*chanceForPurple

The next one to consider is is Diamond. As passing the diamond check skips the gem stone ore check, so it cannot be included in the chance. To be a diamond, it must pass the diamond check, which skips the gem check, and it must fail every other check. This gives:

   diamond = (1-chanceForOre)*(chanceForDiamond)*(1-chanceForPurple)*(1-chanceForMystic)*(1-chanceForStone)

While calculated in quite a different way, the chance to find a diamond node is quite comparable to the chance to find a node of another gem type. And finally, the only other option is a normal rock. This could be calculated as whatever is left over, but for completeness, it must fail every check.

      rock = (1-chanceForOre)*(1-chanceForDiamond)*(1-chanceForGem)*(1-chanceForPurple)*(1-chanceForMystic)*(1-chanceForStone)

Due to the interaction between the different checks it is hypothetically possible for the chance for one of these to be found increasing to decrease the chance of finding others. This is observed with the increasing chance to find ore reducing the chance to find mystic stones and gem nodes, and after a high enough level, also reducing the chance to find diamonds and gem stones; this also reduces the chance of finding dark grey rocks and rocks. Additionally, the increase in chance of finding these valuable items due to luck or mining level reduces the chance of finding dark grey rocks and rocks, but does not parasitically affect each other, e.g. a higher daily luck will increase your chance of finding diamonds, gems, mystic stones and gem nodes, and will decrease the chance of finding dark grey rocks and normal rocks.

Ores From Rocks

If a normal rock is generated, there is still a chance to obtain ore from it. There are 4 different rocks which can be generated, which have an equal chance. When the rock is broken, the code in StardewValley.Locations.MineShaft::checkStoneForItems will potentially call StardewValley.Locations.MineShaft::getOreIndexForLevel to have ore drop. The key parts of the code are:

    double chanceModifier = who.DailyLuck / 2.0 + (double)who.MiningLevel * 0.005 + (double)who.LuckLevel * 0.001;
	double oreModifier = ((tileIndexOfStone == 40 || tileIndexOfStone == 42) ? 1.2 : 0.8);
    if (r.NextDouble() < 0.05 * (1.0 + chanceModifier) * oreModifier) {
		if (r.NextDouble() < 0.25 * (double)((!who.professions.Contains(21)) ? 1 : 2)) {
			Game1.createObjectDebris(382, x, y, who.UniqueMultiplayerID, this); //coal
		}
		Game1.createObjectDebris(this.getOreIndexForLevel(this.mineLevel, r), x, y, who.UniqueMultiplayerID, this);//ore
	} else if (r.NextDouble() < 0.5) {
		Game1.createDebris(14, x, y, 1, this);
	}

This results in a chance to find ore of 5.1% at worst, and 5.7% at best; with a corresponding 47.45% to 47.15% chance to obtain stone. If it would generate ore, then there is a 25% chance to obtain coal, doubled to 50% with the Prospector profession. This results in approximately a 1% chance to get coal from a rock.

Then inside StardewValley.Locations.MineShaft::getOreIndexForLevel, the following code is run to obtain the ore:

	if (r.NextDouble() < 0.01 + (double)((float)(mineLevel - 120) / 2000f)) {
		return 386; //Iridium
	}
	if (!(r.NextDouble() < 0.75)) {
		if (!(r.NextDouble() < 0.75)) {
			return 378; //Copper
		}
		return 380; //Iron
	}
	return 384; //Gold

The chance to obtain iridium ore starts at 1.05% at floor 1, and increases linearly to 100% at floor 1980. When combined with the chance to get ore, this starts at an overall chance to get iridum ore from rocks on floor 1 betwen 0.0536% and 0.060%. In the event it is not iridium, then there is a 75% chance for it to be gold, an 18.75% chance for it to be iron, and a 6.25% chance for it to be copper.

Links to Desmos Graphs

You can access an interactive graph on Desmos via the links below, with the links having a some options preselected.

Desmos Link	Description
https://www.desmos.com/calculator/uwi9hfdjvv	Metal ores vs floor
https://www.desmos.com/calculator/iopaqgwsvs	Gemstones, gem nodes, dark grey rocks (stone ore) and mystic stones vs floor. Note that some values have been scaled to keep it on the same graph.
https://www.desmos.com/calculator/ngyjsb1b0m	The effect of daily luck (including special charm) on the chance normalised to their reference value
https://www.desmos.com/calculator/72efyqudvu	The effect of mining level (including buffs) on the chance, normalised to their reference value

When not being used as the x axis, the values of daily luck, mining level and floor are controlled by a variable in the left pane and are used to calculate a reference. Initially these are set to floor 100, a daily luck of 0.025 (average daily luck with special charm) and a mining level of 10.

History

• 1.6: chooseStoneType renamed to createLitterObject. Additional difficulty can now be 2. Calico statues introduced.